We’ve got something for everyone here in Features — people stories, off-the-beaten-path kind of stories, science-in-action sagas. Take your pick!
Looking for more fun stories about science? Explore the basics of electricity and magnetism and the exciting discoveries that magnets enable in easy-to-understand language at Magnet Academy.

Read updates from MagLab faculty researcher Lydia Babcock-Adams as she journeys aboard the Research Vessel Roger Revelle on a National Science Foundat…
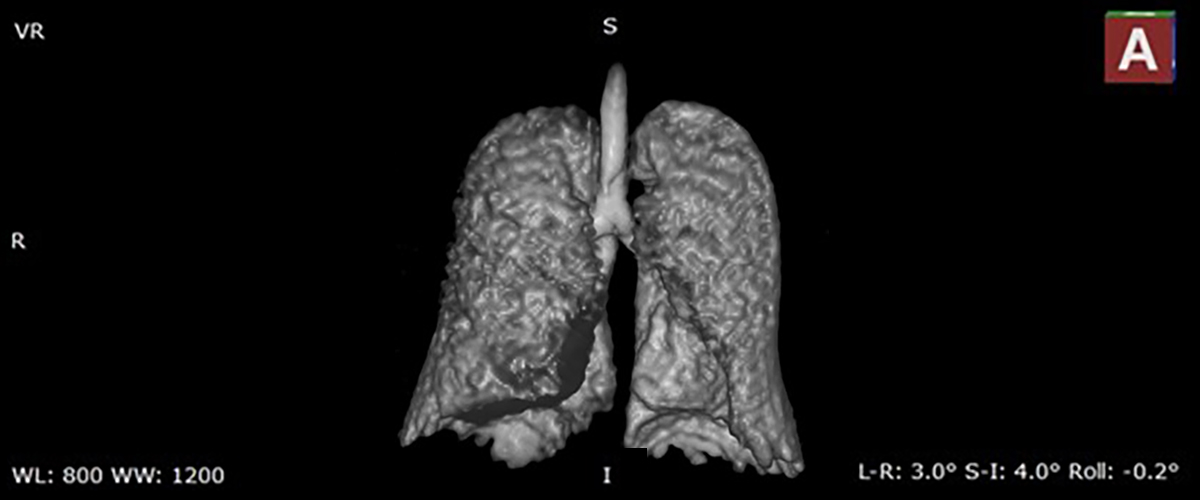
MagLab researchers and doctors at the University of Florida are testing a new MRI technique that can deliver images of the lungs like never before

The halls of the MagLab are filled with world-class scientists and sometimes even celebrities!
New research is a first step toward understanding how a certain protein may help tuberculosis bacteria survive.
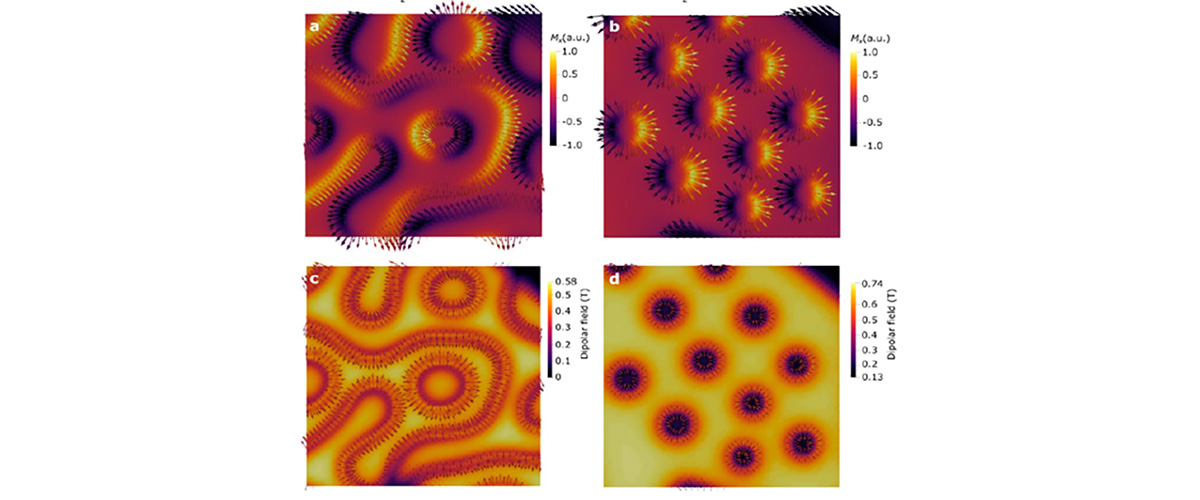
Tangles of interlaced magnetic fields hold promise for use as a basic unit in electronic information storage and quantum computing.

Thin, flexible, strong: MagLab research on the marvel of insect wings
Chemist Danna Freedman explains superposition, decoherence and how they all add up to the most fun you could have with science.

Researcher digs below the coronavirus's membrane in search of another layer of infection-causing proteins.

Step No. 1 of the scientific process is: Ask a question. Sometimes, when things gets rocky, that means asking for support.

A team of researchers pulls off a daring data caper in Delaware Bay, swiping secrets about the movement of molecules between air and water.

For membrane protein expert Tim Cross, solving the structure of a misunderstood protein put retirement on hold.

The virus that causes COVID-19 has thousands of potential drug targets. A global team is on a hunt for the best candidates.

A team of experts believes stem cells could be a route to a fast, effective therapy.

A deeper understanding of petroleum molecules is shedding a harsh light on how some of them behave in our environment.

A team tackling some gnarly physics using tricky techniques rounds a critical corner. Joy ensues. Then, back to work.

Researchers put little permanent magnets into large electromagnets to find out how to make them better.
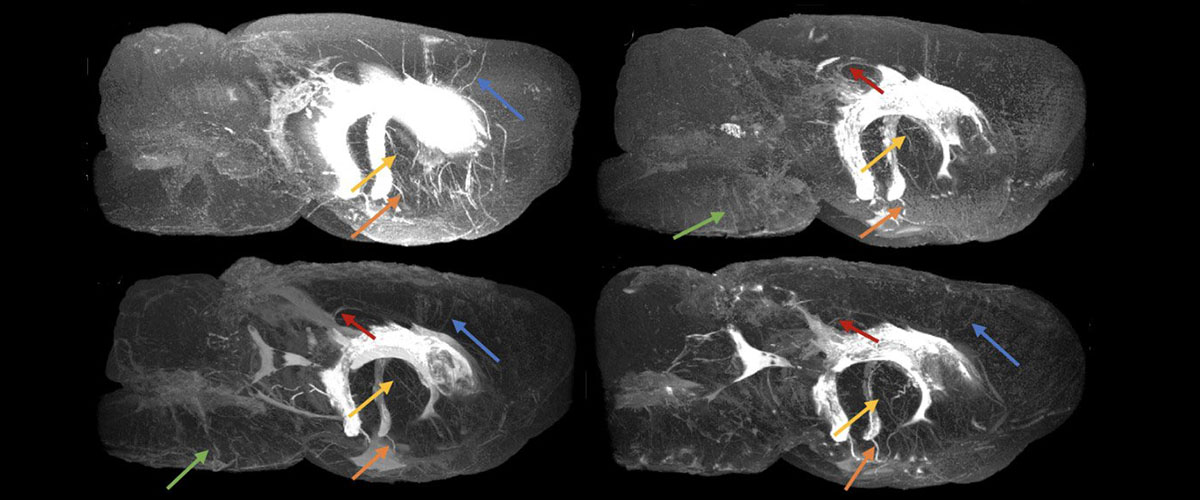
Using advanced MRI, a mechanical engineer tackles the question: "Why do you have these big fluid spaces in your head?"

The world's largest particle collider is getting even larger, and magnet labs are helping lay the foundation.

Some manmade chemicals feature bonds so strong they could last forever. And that's a life-threatening problem.
Scientists are using powerful magnets to learn how to better detect, treat and track the second leading cause of death worldwide.

What hides behind the elegantly simple line that describes the relationship between temperature and electrical resistance in certain materials? For so…

Florida scientists are helping coral protect itself against nitrogen overload.
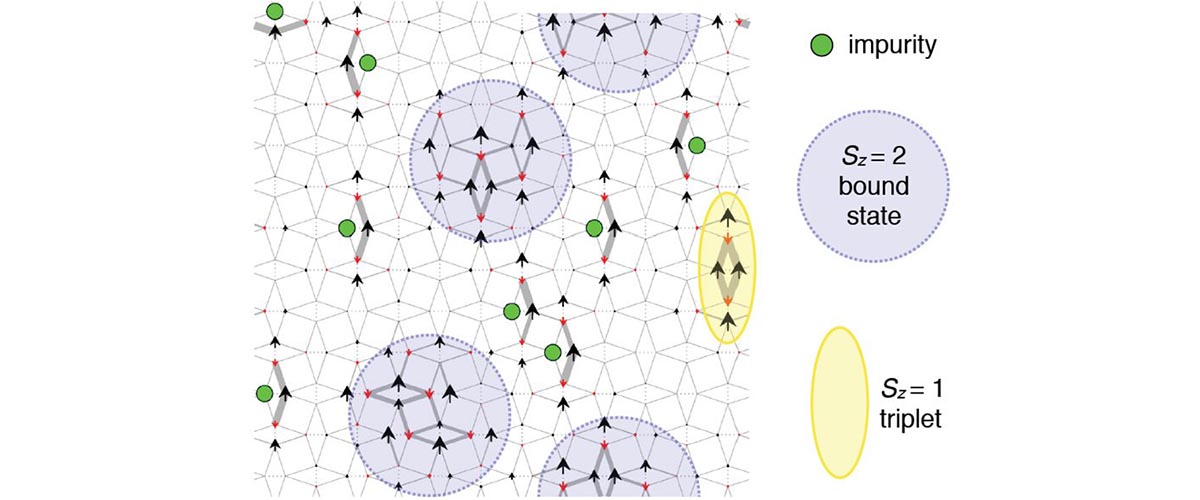
When physicists studied a superconducting material at very high fields, they were pleasantly amazed by what they saw.

Can thin films be designed for future quantum technologies? With a prestigious prize from the National Science Foundation, MagLab physicist Christiann…

With a prestigious prize from the National Science Foundation, MagLab chemist Yan-Yan Hu hopes to boost the performance of materials used in batteries…

Two MagLab teams tried marrying vastly different technologies to build a new type of magnet: the Series Connected Hybrid. Decades later, has the oddba…
Located in a region prone to hurricanes, the National MagLab is ready to weather any storm.

Thanks to the MagLab’s expertise and unique instruments, a geochemist finds a treasure trove of oil-spill data buried beneath the sea.

Researchers talk about their favorite mentors and how they made a difference.

Scientists probing the exotic, 2D realm are discovering astonishing behaviors that could revolutionize our 3D world.

What happens when a kid with ADHD sustains a concussion? Using high-field magnets, researchers are working to find out.
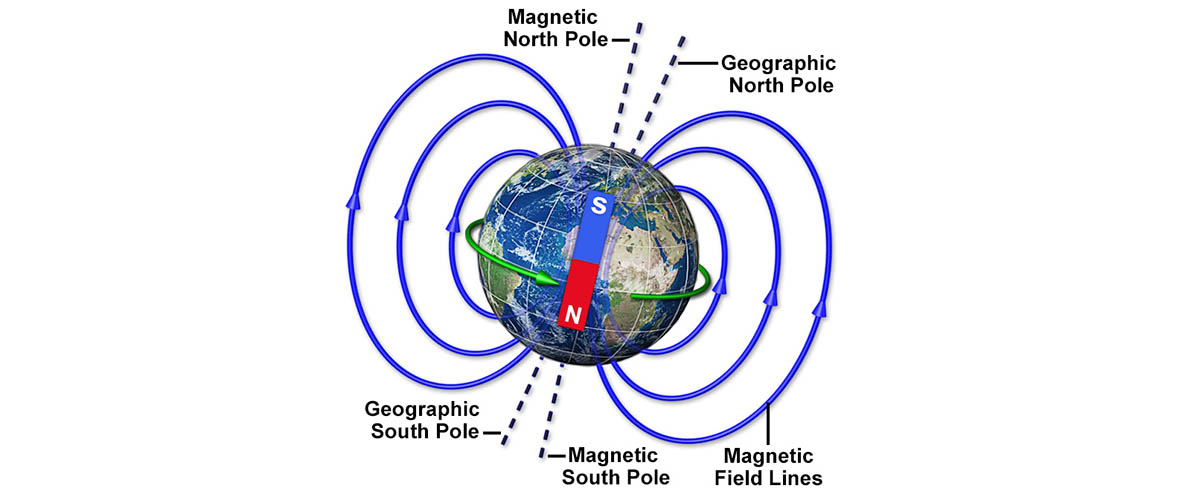
Keeping track of where on earth our poles are is practically a full-time job.

Water samples collected from the heart of Africa contain clues about carbon cycling worldwide.

If engineers build stronger magnets, scientists promise they will come … and that discoveries will follow.

Several materials are in the running to build the next generation of superconducting magnets. Which will emerge the victor?

A technique called dynamic nuclear polarization is hitting its stride, using electrons to shine a light on complex molecules.

MagLab experts fine-tuned a furnace for pressure-cooking a novel superconducting magnet. Now they're about to build its big brother.

How is science like a team sport? From physics to chemistry to biology, it takes a squad to make progress in an increasingly interdisciplinary world.…

How do you keep the world's largest magnet lab clean? With a super-sized cyborg, of course!
Looking for something to give you the edge in your research? Join the team.
Members of a sprawling science team piece together the puzzle of biochar, a promising tool in the fight against global warming.

Using high-field electromagnets, scientists explore a promising alternative to the increasingly expensive rare earth element - neodymium - widely used…
For great research to spread through the world, it takes a lattice.
How do science innovations make it from the laboratory into your life?
In physics, researchers are probing different kinds of super small nano-molecules for properties that will lead to the next generation of electronics.
Scientists are working to understand the complex reactions that create nanocages, work that could help uncage new drug delivery and energy options.

How is nano science advancing door-to-door drug delivery, but on the cellular level?

Undergrad streamlines maintenance routine with touch-screen technology

Looking for ways to make better superconductors for the next-generation particle accelerators, a young scientist homed in on how they were heat-treate…

Young scientists learning the ropes find they get by better with a little help from their fellow students, postdocs and colleagues.

Studying dissolved organic matter helps us better understand our changing planet.

Why do electrons behave bizarrely near the surface of some materials? At the dividing line between two things, there’s often no hard line at all. Rath…

How can the barrier between oil and water in emulsions be broken down? When things overlap, you often get more than the sum of those parts. Or as one …
Which adjoining ingredients can yield a better lithium ion battery? Learn about a scientist who is pushing the boundaries of knowledge by exploring th…

Borderline biology? Crossover chemistry? Scientists are working on the edge of their fields to learn how proteins police the walls of cells.

The culmination of years of hard work, the dissertation defense is as much an ordeal as it is a ritual.
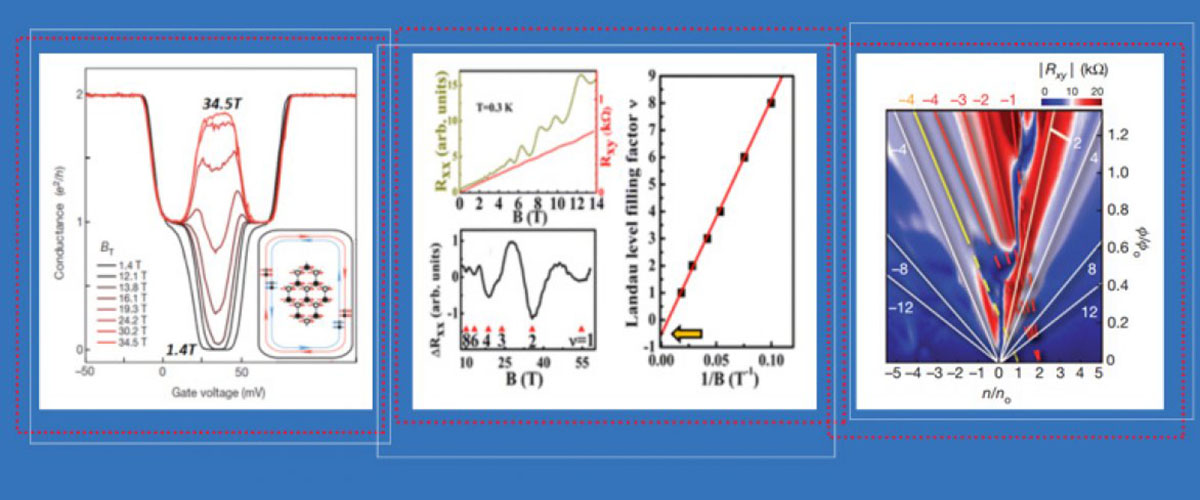
At the National MagLab, scientists have been experimenting for years on materials first dreamed up by the newest physics Nobel laureates decades ago.

How do you measure the bite force of a prehistoric megabeast? At the National MagLab.

Deep in their beautiful lattices, crystals hold secrets about the future of technology and science. Ryan Baumbach aims to find them.

Time off from the lab can recharge batteries, inspire new insights and give the brain a break — even when a little science sneaks in.

When a grad student's first publication lands in the top-tier journal Nature, you can bet it's not beginner's luck.

When it comes to science, is there a pot of golden data waiting to be discovered at the end of the rainbow?

At research conducted at the MagLab, a young geochemist uncovers the surprisingly violent origins of a meteorite.

How do you strike a balance between competition and collaboration in science?

What is homogeneity and why is it so important to scientists? Learn how homogeneous magnets make data clearer by milking the magnetic field strength f…

Postdocs face big challenges as they learn the ropes of real-life science. The MagLab and other institutions are doing more to help them make the most…

When a Florida teacher had the chance to spend a second summer doing research at the MagLab, he didn’t have to think twice.

A material that you may never have heard of could be paving the way for a new electronic revolution.

What are the ten coolest (and most surprising) things about the world's strongest MRI magnet?
Many scientists and engineers at the MagLab moonlight as moms and dads. What can they teach the layperson about raising scientists — or better kids?

With just a week to use a magnet, researchers work around the clock to eek out as much data as possible.

High school intern Kyle Buchholz uses his time at the MagLab to learn science hands-first, rather than head-first.

Paul Rigel, a Florida middle school teacher, talks about his six weeks working at the MagLab's microanalysis lab.

Gerardo A. Nazario, a Research Experiences for Undergraduates (REU) intern, talks about his eight weeks working at the MagLab and at the MagLab's Appl…

Petroleum engineer Alicia Calero, a former participant in the lab's Research Experiences for Undergraduates program, talks about two MagLab scientists…

MagLab scientist Bob Goddard talks about his 17 years as a mentor.

After a series of frustrating failures, a team of MagLab scientists realized they were tackling the wrong problem.

Sodium MRI techniques point to better cancer treatments.

Teenagers spent Fridays at the MagLab this fall working on a research project.

These teachers went from their classroom to the lab to spend their summer break learning science skills.
Students take field trips designed to inspire girls to pursue careers in science.
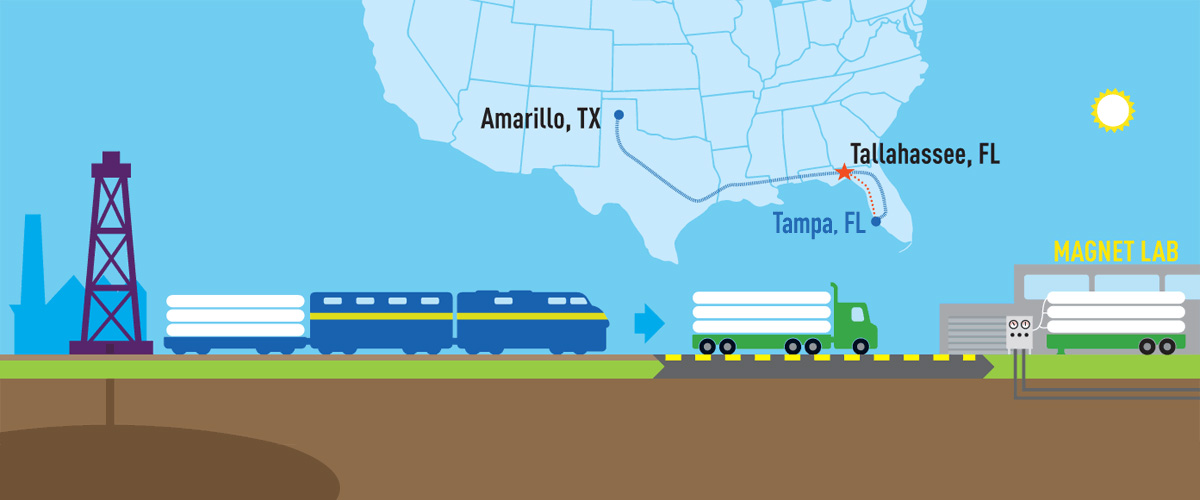
A helium-recovery project means major savings — and more focus on science.

Two scientists put their heads together and created a machine that speeds along magnet production.

Anyone can have a career in science. Here are some tips and MagLab programs that will help you hone science skills for students of every age and stage…

From Superman materials to tree-bark gasoline, the MagLab is on the front line of energy research.

A scientist taps the sun's ancient power for cutting-edge research.

Our magnets are like world-class athletes: powerful, but to stay in scientific shape, they need to eat and drink – a lot.

With the most powerful MRI machine in the world, you can do cutting-edge studies on neurodegenerative diseases, cancer, tobacco use, muscles and more.

Building the world's best resistive magnets requires clever engineering, top-notch science, superior materials and an obsession with quality control.

MagLab machinists collaborate closely with scientists to create one-of-a-kind magnet parts that make possible experiments done nowhere else in the wor…