Qubit Q&A

Danna Freedman

Are you curious about qubits, those cutely named building blocks of tomorrow's quantum information technologies? Well, join the qubit queue: Who isn't interested in the powerful machines that, in the decades to come, will revolutionize communication, sensors, measuring, cryptography — and who knows what else?

For most lay folk, qubits (or quantum bits) are a lot harder to understand than the conventional 1's and 0's we use to store or transport everything from tweets to spreadsheets. But those binary bits are destined to become digital dinosaurs, as scientists work to develop qubits that will displace them.

How do they work and when can you expect to find qubit-powered technology on your desk? Northwestern University chemistry professor Danna Freedman agreed to field our qubit queries. Freedman's group uses high magnetic fields and other tools to assemble and study molecules that could one day function as qubits. Read on and take your qubit cues from Freedman.

We're about to get quantum! What advice can you give readers to prepare them to go from today's familiar classical realm to this quantum realm where everything is super weird?

Quantum completely defies our intuition. The fundamental idea is, when you enter quantum, you enter a space where nothing is absolute. Everything exists in a sort of probability distribution. So instead of saying, "We know the answer at every second," we say, "We know that it is this likely, under these conditions." This is something that makes sense when you're talking about a population, but a lot less sense when you're talking about a single particle.

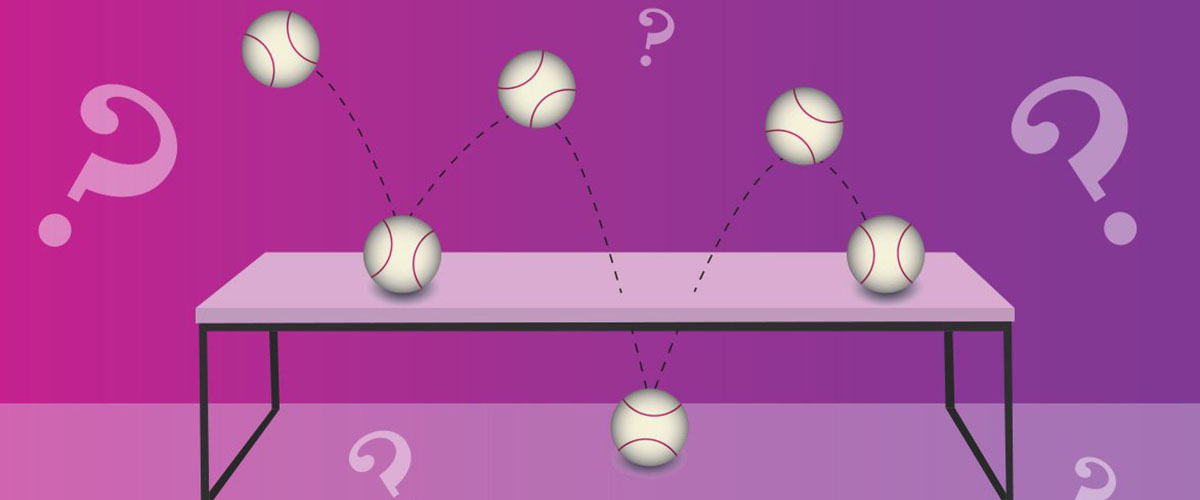
If we think about a baseball bouncing on a table, it will always bounce up and down on the table. In the quantum space, if it was an electron rather than a baseball, you could picture it bouncing up and down, the way that your intuition expects. But every once in a while, it would just fall through the table. And that's completely crazy. It doesn't make sense that at some probabilistic point, the electron will dive through the table. This is a really fun and crazy space that we get to exist in, this quantum universe.

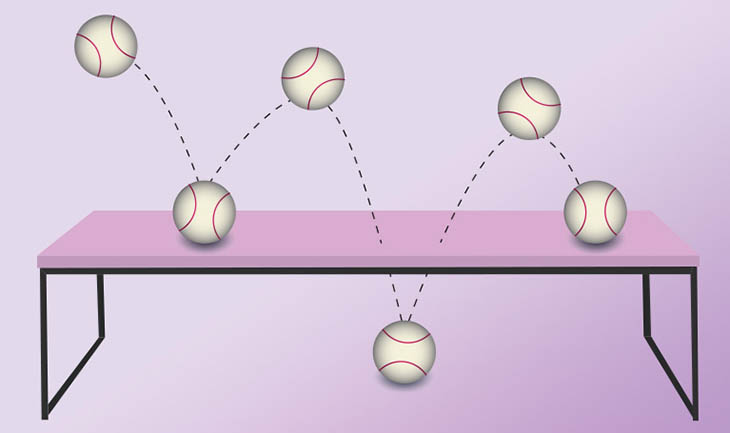
Image credit: Caroline McNiel.

Today's computers are based on basic units of information called bits, streams of electrical and optical pulses that represent information as either as a 1 or a 0. The term "bit" comes from "binary digit." But qubits aren't binary at all. Can you explain this?

Instead of thinking about 1 and 0 as numbers, let's instead map them onto a sphere. Let's go back to our baseball, and we'll put a 1 on top and a 0 on the bottom. Now we have these two states that we've defined in a discrete way, and we can say we're going from one to the other.

Now let's move from a classical to a quantum space, where you say that this individual unit, this quantum unit, exists in all possible spaces. Instead of being limited to just two spots on the ball, your two values could be located anywhere on the sphere's surface. Instead of two states, you have the infinite number of states that form the surface of the sphere, and this is effectively how you can think about a qubit.

If you prefer to think about quantum mechanics more from a wave perspective, you can imagine two waves combining, and every combination of those waves existing at once.

How does that property of superposition — of existing in multiple places at the same time — make qubits so powerful?

If you have 1,000 quantum bits in your quantum computer, each of which can be either a 0 or a 1, your quantum computer can represent all 2¹⁰⁰⁰ states simultaneously [which is an unprintably large number! -Ed.]. The computer does not need to proceed through each possibility sequentially. If each bit has multiple values (say “m” values), then the quantum computer can try out m¹⁰⁰⁰ states simultaneously, and this number goes up insanely rapidly as m goes from 2 to 3 to 4, etc.

What kind of problems is that useful for?

To be glib about it, any problem for which a quantum algorithm has been written.

One important class of problems is the needle-in-a-haystack type problem, where you're searching over multiple configurations for one that works. We see this in everything from planning where sports teams will play each other to protein folding and configuration to doing high throughput analysis of drug protein interactions.

Then there's the class of problems that exists because of an algorithm. Back in 1994, mathematician Peter Shor invented a quantum algorithm for factoring large numbers (Shor's algorithm). This is really important, because the way that we encrypt data is based on the fact that we can't factor large numbers quickly. Shor's algorithm could fundamentally break encryption. This is one of the most well-established applications of quantum computing.

Could you talk about the challenges of superposition?

With a classical computer, you define a bit that's 0 or 1, and you don't worry about it decaying: You don't worry that it will leave its 0 or 1 state.

For a quantum computer, we have a whole host of different challenges. The first one is that our bits are put into this fragile superposition state, which is a combination of 1 and 0 or up and down. The first thing that we have to do is make sure that the bits live long enough in this state. The collapse of the superposition state is known as decoherence, and is caused by interactions in the environment. So here we have the fundamental paradox and challenge of anything in a quantum universe: If you take a qubit, and you fully isolate it from the environment, it will live for a very long time — it will have a very long coherence time. But for any application of quantum information science, you need qubits to interact.

The next key challenge relates to the lifetime of these qubits, because when superposition collapses, errors occur. When you perform a quantum operation, it's inherently probabilistic: You might get the answer 99% of the time. Currently one of the approaches to quantum computing is to develop quantum error correction, which helps you get the right answer all the time.

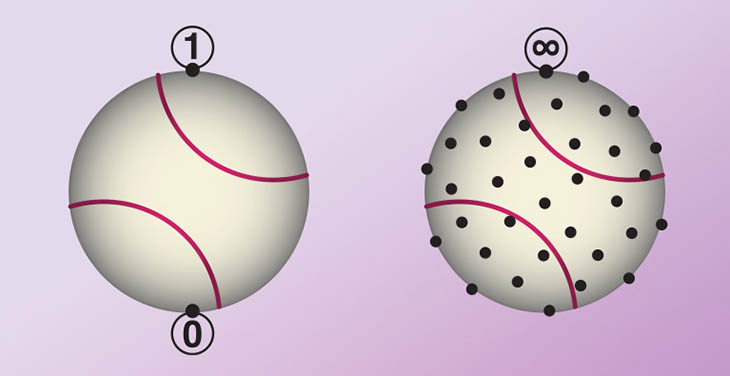
Image credit: Caroline McNiel.

How do you make a qubit?

A qubit is fundamentally anything that can exist in a superposition state: up and down, 1 and 0. There are a lot of different candidates for qubits.

One is a superconducting qubit. A lot of companies such as IBM and Google have invested in this technology, and it's compatible with current fabrication technologies.

Another large category of qubits is spin-based qubits. "Spin" refers to a property that some subatomic particles, including nuclei and electrons, have. In simple terms, you can imagine those particles spinning around an axis, like a top that can spin right side up or upside down. Scientists exploit that inherent two-state system in an up or down spin as a qubit.

There are electron spin candidates and nuclear spin candidates for qubits. In the nuclear spin category, the University of New South Wales is leading the charge in creating artificial atoms embedded in silicon. Another class of spin-based qubits is the defect-based materials. In these, the qubits are atoms residing within semiconductors or insulators. One example of such a material is the highly successfully anionic nitrogen-vacancy centers in diamonds. These systems are generally fabricated by implanting ions in the diamond’s crystal lattice.

Other important categories of qubits are cold atoms, where an atomic transition is used as a qubit, and topologically protected qubits, which are inherently protected from error. Also there are the so-called flying qubits, because physicists are really good at naming things. Those are just photons.

In my lab we work with spin-based qubits that are based in molecules. We're working on making systems similar to both the spin-based qubits in silicon and the defect-based qubits. But instead of top-down fabrication, we're doing bottom-up fabrication.

Could you describe that approach?

We're using primarily electronic spins, but we're also looking at nuclear spin as a qubit. When you synthesize a molecule, you get to put every atom exactly where you want. Not only that, but you don't synthesize a molecule, you synthesize a lot of molecules, which offers potential for scalability. Every molecule in a sample is identical. When you take a tablet of aspirin, you take it for granted that every single molecule in that tablet of aspirin has exactly the same structure. And you also take it for granted that the bond distances between the atoms are precise down to a ridiculous level. In quantum applications, this high level of precision is absolutely essential.

Molecules allow you to have a high level of tunability for different applications. The design criteria for a quantum sensor and for a quantum computer do not match up perfectly, but with molecules, you can modulate the function by tweaking the molecule’s structure.

We synthesize our systems using standard chemical synthetic protocols, very similar to how you would synthesize a drug candidate in the lab. Then we analyze them, for example at the MagLab, to acquire data about their coherence properties. We can execute hypothesis-driven science with molecules by asking, "If we move this atom, do we expect to increase the coherence time? Or will we decrease the photon contribution to coherence time?" So we can articulate a hypothesis, execute a test and get an answer, which is just really fantastic.

Freedman’s group synthesized these two qubit candidates — [Ni(phen)₃](BF₄) and (Ph₄P)₃[Fe(C₅O₅)₃] — and measured them at the National MagLab.

Image credit: Chung-Jui Yu

So you build different types of molecules and then run them through these tests?

Yes. And some of them had really good properties. For example, we demonstrated that molecules can have coherence times that are comparable to other spin-based qubits, about a millisecond. That was a really important concept and demonstrated that molecules are kind of in the game as qubit candidates.

We are currently working on different readout approaches — ways that you can read the data stored in a qubit — and making molecules compatible with established approaches. One way that you can see what the qubit says is using a magnetic field, by putting it in one of the instruments at the MagLab. In the defect-based candidates, you use light. There are different materials for building qubits, and then there's also the established technological infrastructure for determining what those materials are telling us. Creating new materials that integrate with a lot of these different readout approaches is very important.

If we can, from a molecular perspective, integrate with established readout technologies, then that really pushes the research forward.

What are the biggest obstacles to developing quantum information science technologies?

On the quantum computing side, in my opinion, it's error correction. You get the right answer, but only some percent of the time.

More broadly in quantum information science, the biggest obstacle I would say is materials, tunable materials. The type of candidate that you would use for quantum metrology — exploiting quantum properties to execute precise measurements — would have fundamentally different properties than something that you want for one of these fantastical applications like a quantum internet. In both cases you're using materials where you can manipulate the quantum properties. But you need different forms of interaction and different properties for both.

So when will we see some of these technologies?

I don't think there's going to be one day when all these technologies become a reality. In terms of quantum computing, we're in an era called the Noisy Intermediate-Scale Quantum or NISQ. There are certain classes of problems that we can look at with these early quantum computers, but it's not necessarily the type of problem that is of the largest interest to the general public. I think it will take a couple of decades to access societally transformative problems.

As we scale up, we're going to hit interesting problems along the way. There are a lot of academic problems where you can begin to make a difference. Some of those are even in my own field of chemistry where, by coupling quantum computing modeling of problems with classical modeling, you can start to get more precise solutions to problems. You might even be able to push toward understanding fundamental processes of interest, like catalysis. Many companies that are invested heavily in quantum computing have their own published projections, and I would defer to some of these ideas. This is a highly interdisciplinary field, and my specific area of expertise is in constructing the core materials for quantum information science rather than implementing any quantum computation.

In quantum sensing, there have already been really interesting implementations. There's some really nice work on using qubits to map magnetic textures called skyrmions and on mapping protons in biomolecules. One of the aspirational goals of quantum sensing is to move to single molecule magnetic resonance, which is being able to map out the structure of one molecule in an ensemble. I think that's also a couple of decades away, but every step toward that will be a gigantic scientific achievement.

What got you into this line of research?

Scientists don't know the answer! I love problems where we can create genuinely new science. We can define so many questions and answer them and create new materials using the fundamental scientific principles of chemistry to explore an entirely new area. It's pretty much the most fun you can have with science.

Still curious about qubits?

Read these articles by Freedman's group.

Michael K. Wojnar, et al, Nickel(II) Metal Complexes as Optically Addressable Qubit Candidates, J. Am. Chem. Soc. (2020).

Joseph M. Zadrozny and Danna E. Freedman, Qubit Control Limited by Spin–Lattice Relaxation in a Nuclear Spin-Free Iron(III) Complex, Inorg. Chem. (2015).

Interview by Kristen Coyne