We know you've heard of the "frozen fractals" that Elsa sang about in the popular animated DISNEY movie.
But what exactly is a fractal?
A fractal is a geometric shape with a seemingly never-ending repeating pattern. Created by repeating a procedure (or iterating an equation), fractal shapes are satisfyingly similar at every level of magnification. A shape does not have to be exactly identical to be classified as a fractal. Instead shapes that display inherent and repeating similarities are the main requirement for being classified as a fractal.
At the MagLab, scientists use powerful magnets to look for fractal patterns in unique materials as they learn more about the fundamental properties of matter.

Left: This fern consists of many small leaves that branch off a large one. Right: This Romanesco broccoli consists of smaller stems spiralling around a large one.

Sierpiński triangle where there are an infinite number of small triangles inside the large one. The Sierpinksi triangle is constructed using patterns.

The Mandelbrot set is one of the most famous shapes in mathematics named for Benoît Mandelbrot. The Mandelbrot set is based on an equation.
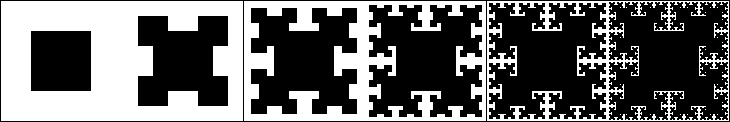
T-square (T-fractal)
Why are fractals important?
Fractals help us understand important scientific concepts in physics, biology, and geology, such as the structure of freezing water, the pattern of brain waves, or the way bacteria grow. Their formulas help researchers analyze complex patterns and have been crucial to the workings of our everyday life. Wireless cell phone antennas even use a fractal pattern to pick up a wider range of signals.
One classic example of a fractal is known as the Sierpiński triangle, which contains an infinite number of smaller triangles inside it in a repeating pattern. You can draw one for yourself!
What you’ll need for drawing Sierpinski Triangle:
- A sheet of paper
- Pencil and/or pen in different colors
- Ruler
What you'll do:
1. Draw an equilateral triangle (that is the a triangle that is the same on all sides).

2. Draw a point in the middle of each of the three sides of the triangle, and then connect those points to form a new triangle. Now we have four smaller triangles - one in the middle and three in the corners. The triangle in the middle is pointing down, whereas the other three triangles are pointing up.

3. Repeat Step Two for the outer three triangles, drawing a point in the middle of each of the sides and connecting the points to form a new triangle.




4. Each time we repeat step 2 is called an iteration, or how many times we’ve repeated the same operation. We now have a big triangle in the middle pointing down, and 3 smaller ones pointing down. If we were to stop here we’d color each of the triangles pointing up black, and leave the triangles pointing down white. If we continue to repeat step 2, however, we would draw a point in the middle of each side of the 9 triangles pointing up and connect those points to form new triangles, repeating the process for each of the newly created triangles that are pointing up. If you want to stop here, color each of the triangles pointing up black, and leave the triangles pointing down white.
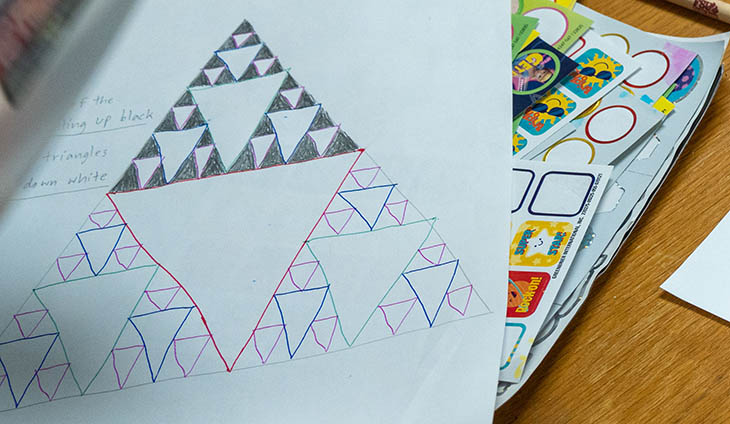
5. Challenge: How many iterations can you do?
Fun experiment: Design your own fractal
- Draw a large version of a different shape.
- Choose a rule that you'll repeat over and over.
- Apply this rule to your image or shape over and over.
- Keep going until it’s too small to draw the details.
- Share your work.
Did you know?
- Fractal shapes appear in many parts of nature: ferns, trees, snowflakes, and lightning are among the examples.
- The circulatory and respiratory systems of many animals are also fractals.
- The Mandelbrot set is known to be the most famous fractal in modern mathematics, mainly because of its haunting beauty.
- The Sierpiński triangle is named for Polish mathematician Wacław Franciszek Sierpiński, who studied its mathematical properties. It has been used as a decorative pattern for centuries.